Spherical capacitor and Cylindrical capacitor

Objective :
To find the capacitances of Spherical and Cylindrical capacitors.

Spherical capacitor

A spherical capacitor consists of a spherical conductor of radius ‘a’, surrounded by another hollow concentric sphere of radius ‘b’.

Suppose charge ‘+Q’ is given to the inner sphere and ‘–Q’ to the outer sphere.


We know that field due to ‘charge on outer sphere’ at an interior point is zero.

Hence, field at a point that lies between the conductors depends only on the charge on the inner sphere.

Thus, electric field between conductors at a distance ‘r’ from the center,

E=Q4πε0r2.


Since charge distribution has radial symmetry, potential difference between two conductors is,

V=Va-Vb

V=-∫abE·dr

Upon integration and substitution of limits, we get potential difference between the conductors,

V=Q(b-a)4πε0ba


Capacitance of spherical conductor,

C=QV

Thus, Capacitance of a spherical conductor comes out to be,

C=4πε0ba(b-a).

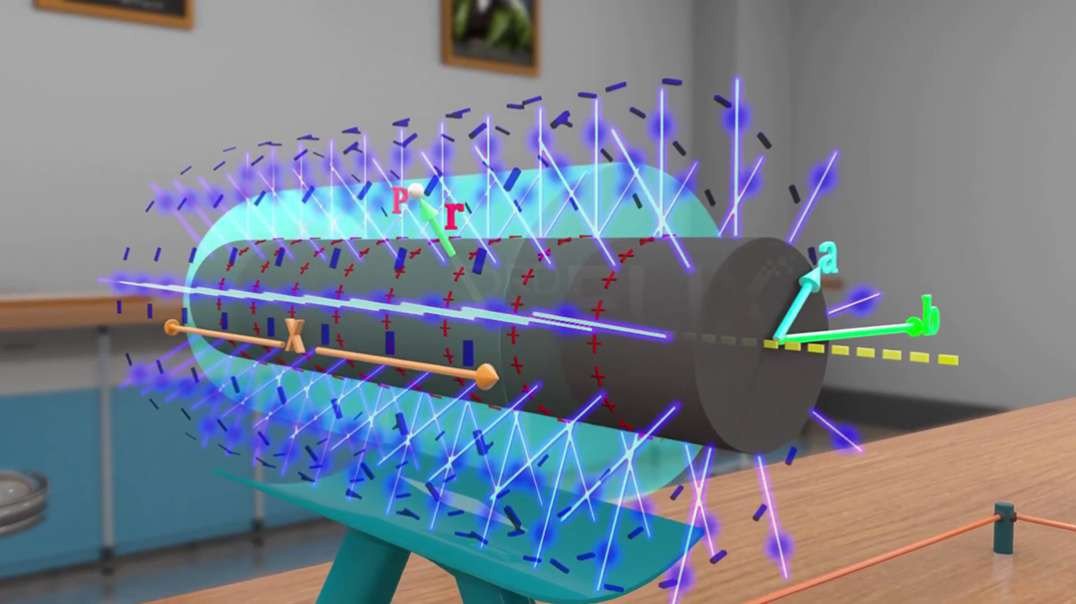
Cylindrical Capacitor :

Consider a cylindrical capacitor of length ‘L’ ; Radius of the inner cylindrical surface be ‘a’ and that of outer surface be ‘b’.

Suppose a positive charge ‘+q’ is placed on the inner cylinder and a charge ‘–q’ is placed on the outer cylinder.

If the cylinder is long, as compared to the separation between its surfaces, electric field at a point between the cylinders will be radial and its magnitude will depend only on the distance from the axis.

Consider a point ‘P’ between the cylinders at a distance ‘r’ from the axis.

To calculate the electric field at point ‘P’, let us draw a gaussian cylinder of length ‘x’ and radius ‘r’.

The flux through the bases of gaussian cylinders is ‘zero’, as electric field is perpendicular to the base.

Flux through the curved part,

ϕ=∮E·ds

=E(2πrx).

The charge enclosed by the gaussian surface,

Qen=Qlx

Thus, from gauss’s law,

E(2πrx)=Qlx/ε0

Which gives

E=Q2πε0rl.

The potential difference between the cylinders is equal to,

V=-∫baE·dr.

Upon solving the equation, we get,

V=Q2πε0llnba.

The capacitance,

C=QV

Which comes out to be,

C=2πε0lln(b/a).

Summary :
Capacitance of a spherical capacitor with radii ‘a’ and ‘b’ is equal to,

4πε0ba(b-a).

Capacitance of a cylinder capacitor of length ‘L’ with radii ‘a’ and ‘b’, is equal to

2πε0lln(b/a).